De Gaussiaanse grafiek en de sociologie
(Deels ook in Groep en individu
 )
)
In de Gaussiaanse grafiek,
algemeen
 zijn de technische details van de verdeling van menselijke eigenschappen zoals
die van lengte uitgewerkt. Die verdeling geldt voor vrijwel alle menselijke
eigenschappen, en ze geldt ook ook voor de verdeling van die eigenschappen
binnen groepen. Het geldt dus ook voor de verdeling van lengte bij Nederlanders
en Japanners, die dus kunnen verschillen in gemiddelde en spreiding.
zijn de technische details van de verdeling van menselijke eigenschappen zoals
die van lengte uitgewerkt. Die verdeling geldt voor vrijwel alle menselijke
eigenschappen, en ze geldt ook ook voor de verdeling van die eigenschappen
binnen groepen. Het geldt dus ook voor de verdeling van lengte bij Nederlanders
en Japanners, die dus kunnen verschillen in gemiddelde en spreiding.
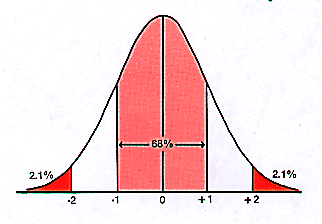 De
normale verdeling is een geleidelijke verdeling, dus zijn er geen vastomlijnde
grenzen te trekken om aan te geven waartussen de lengtes van Japanners en de
Nederlanders zich bewegen. Maar daar komt de regelmaat van de normale verdeling
te hulp. Alle eigenschappen zijn gedefinieerd door het gemiddelde en de
standaarddeviatie, dus alles wat we hoeven doen in in zowel de grafiek van de
Japanners als de Nederlanders een punt te kiezen met dezelfde waarde voor de
standaarddeviatie. Dat kan een van de gehele waarden zijn, 1 voor de tweederde
van de bevolking, of de 2 voor de 95 procent van de bevolking, of wat voor
waarde dan ook, als je maar voor Japanners en Nederlanders dezelfde waarde
neemt. In dit geval zou je zo veel mogelijk van de bevolking mee willen nemen,
dus is twee een logische keuze. Het stukje lijn van -2 to +2 in de Gaussianse
grafiek boven komt dan overeen met de balkjes in de grafieken van Groep en
individu , een voor de Japanners en een voor de Nederlanders . De
normale verdeling is een geleidelijke verdeling, dus zijn er geen vastomlijnde
grenzen te trekken om aan te geven waartussen de lengtes van Japanners en de
Nederlanders zich bewegen. Maar daar komt de regelmaat van de normale verdeling
te hulp. Alle eigenschappen zijn gedefinieerd door het gemiddelde en de
standaarddeviatie, dus alles wat we hoeven doen in in zowel de grafiek van de
Japanners als de Nederlanders een punt te kiezen met dezelfde waarde voor de
standaarddeviatie. Dat kan een van de gehele waarden zijn, 1 voor de tweederde
van de bevolking, of de 2 voor de 95 procent van de bevolking, of wat voor
waarde dan ook, als je maar voor Japanners en Nederlanders dezelfde waarde
neemt. In dit geval zou je zo veel mogelijk van de bevolking mee willen nemen,
dus is twee een logische keuze. Het stukje lijn van -2 to +2 in de Gaussianse
grafiek boven komt dan overeen met de balkjes in de grafieken van Groep en
individu , een voor de Japanners en een voor de Nederlanders .
Wat geldt voor de lengte van Nederlanders en Japanners, geldt voor alle
eigenschappen van groepen. Op geen enkele wijze is voor wat voor eigenschap dan
ook een vaste waarde voor een kenmerk te kiezen dat kan dienen als onderscheid
tussen de twee groepen: er zijn altijd uitzonderingen - er zijn altijd Japanners
te vinden die langer zijn dan iedere Nederlander. Mits, mits men niet te dicht
in de buurt komt van de grenzen, want dan wordt het wel steeds moeilijker - heb
je al een extra lange Nederlander om mee te beginnen, wordt het extra, extra
moeilijk een nog langere Japanner te vinden.
De eerste belangrijke les daaruit voor toepassing in de wat gevoeligere
toepassingen is dat het bestaan van welke hoeveelheid uitzonderingen op de regel
dan ook, dit op geen enkele wijze een ontkrachting is van het feit dat de
gemiddelden een verschillende waarde hebben. Neem als voorbeeld van een gevoelig
dossier dat van een verschil in criminaliteit tussen twee groepen. Bij de ene
groep, A is een op de duizend een crimineel, bij de tweede, B, is 2 op de
duizend crimineel. Men kan dat dus vertalen als: de ene groep is tweemaal zo
crimineel als de andere. Door degenen die bezwaar hebben tegen deze vormen van
sociologie wordt dit bestreden met eindeloos veel verhalen over het aantal
mensen binnen groep B die niet crimineel zijn. Al die verhalen kloppen, net als
de verhalen over Japanners zijn die langer zijn dan Nederlanders kloppen, maar
het heeft op geen enkele wijze gevolg voor de conclusie over de
groeps-eigenschap, voor het gemiddelde: groep B blijft tweemaal zo crimineel als
groep A.
Een andere belangrijke conclusie uit dit verhaal is dat het in de meeste
gevallen onmogelijk is regels voor grotere groepen te ontwerpen die voor
iedereen goed werken. Iedere regel trekt een grens, en het trekken van een grens
in een Gaussiaanse grafiek snijdt altijd door de grafiek, er zijn altijd mensen
die er ten onrechte buiten vallen, en mensen die er ten onrechte binnen vallen.
het enige dat men dan kan doen is redelijke grenzen stellen, bijvoorbeeld 1 of 2
standaarddeviaties, afhankelijk van het soort eigenschap, en de degene die
erbuiten vallen te behandelen op individuele basis. De schoenfabrikant maakt
schoenmachines voor de meeste gewone maten, maar de echte afwijkingen moeten
maar geholpen worden door een schoenmaker die met de hand werkt.
Het laatste voorbeeld laat tevens zien dat de Gaussiaanse grafiek ook
belangrijke gevolgen heeft voor het bestuderen en het besturen van de
maatschappij, waarover meer hier
 , en de mens
, en de mens
 . .
Naar Gauss psychologisch
 , of site home
, of site home
 . .
|  De
normale verdeling is een geleidelijke verdeling, dus zijn er geen vastomlijnde
grenzen te trekken om aan te geven waartussen de lengtes van Japanners en de
Nederlanders zich bewegen. Maar daar komt de regelmaat van de normale verdeling
te hulp. Alle eigenschappen zijn gedefinieerd door het gemiddelde en de
standaarddeviatie, dus alles wat we hoeven doen in in zowel de grafiek van de
Japanners als de Nederlanders een punt te kiezen met dezelfde waarde voor de
standaarddeviatie. Dat kan een van de gehele waarden zijn, 1 voor de tweederde
van de bevolking, of de 2 voor de 95 procent van de bevolking, of wat voor
waarde dan ook, als je maar voor Japanners en Nederlanders dezelfde waarde
neemt. In dit geval zou je zo veel mogelijk van de bevolking mee willen nemen,
dus is twee een logische keuze. Het stukje lijn van -2 to +2 in de Gaussianse
grafiek boven komt dan overeen met de balkjes in de grafieken van Groep en
individu , een voor de Japanners en een voor de Nederlanders .
De
normale verdeling is een geleidelijke verdeling, dus zijn er geen vastomlijnde
grenzen te trekken om aan te geven waartussen de lengtes van Japanners en de
Nederlanders zich bewegen. Maar daar komt de regelmaat van de normale verdeling
te hulp. Alle eigenschappen zijn gedefinieerd door het gemiddelde en de
standaarddeviatie, dus alles wat we hoeven doen in in zowel de grafiek van de
Japanners als de Nederlanders een punt te kiezen met dezelfde waarde voor de
standaarddeviatie. Dat kan een van de gehele waarden zijn, 1 voor de tweederde
van de bevolking, of de 2 voor de 95 procent van de bevolking, of wat voor
waarde dan ook, als je maar voor Japanners en Nederlanders dezelfde waarde
neemt. In dit geval zou je zo veel mogelijk van de bevolking mee willen nemen,
dus is twee een logische keuze. Het stukje lijn van -2 to +2 in de Gaussianse
grafiek boven komt dan overeen met de balkjes in de grafieken van Groep en
individu , een voor de Japanners en een voor de Nederlanders .